キャンセレーション法の賭け方｜数列の作り方と損切りラインの決め方

キャンセレーション法とは、目標とする利益額をいくつかに分割し、法則に従って追加・削除の操作をして全部消えたらセット終了とするベッティングシステムです。

分割数によって難易度が変わったり、追加削除の法則が少し面倒だったりしますが、数列を消化できれば目標とした金額の利益になります。

この記事で分かること

• キャンセレーション法は目標金額を3つ以上に分割して数列を作り、消化できれば設定した金額分の利益になる
• キャンセレーション法は少し難易度が高く、モンテカルロ法を理解していたほうがよい

この記事はおよそ 8分 で読むことができます。

キャンセレーション法とは？

キャンセレーション法は、ライブゲーム・テーブルゲームで利用できるベッティングシステム（マネーシステム）の一つです。「キャンセレーション」は英語で「打ち消す」「相殺する」という意味があり、勝利時に数列を消していくことからその名前が付いています。

先に目標金額を決め、数列を消化できればその金額分の利益になるため、「ゴールが明確な」ベッティングシステムとして人気があります。ただし目標金額を決められることと、有利になることは別です。ハウスエッジ（控除率）そのものは変わりません。

キャンセレーション法と相性が良いカジノゲーム

キャンセレーション法は、当たったときに配当が2倍になるベットを前提にしています。そのため、次のようなゲームと組み合わせて使われます。

• ルーレットの赤・黒、奇数・偶数（18ポケットが埋まる賭け方であれば使えます）
• バカラのプレイヤー
• マネーホイールゲーム（ドリームキャッチャーなど）の「1」

バカラのバンカーへのベットは手数料が引かれて1.95倍になるため、配当が2倍になるプレイヤーに賭けるほうが計算は簡単です。手数料のないノーコミッションバカラであれば2倍で計算できますが、そのぶんバンカーが6で勝った場合の配当が半額（1対2、賭け金を含めて1.5倍）になり、バンカーのハウスエッジ（控除率）は約1.06％から約1.46％へ上がります。また、ブラックジャックはダブルダウンやスプリットなど追加ベットが最適解になる場面があり、それらを使わずに賭け続けると還元率（RTP）が大きく下がります。

キャンセレーション法の使い方（賭け方）

数列の作り方と基本の手順

1セットで獲得したい目標金額を設定します。資金が尽きる前にセットを消化しやすくするため、資金全体の10％程度を目安にするとよいでしょう。今回は「20ドル」とします。

この「20」を3つ以上の数字に分割して一つの数列にします。つまり数列の合計が「20」になるようにする、ということです。数列はどう分解してもよいのですが、小さい数字から左に並べていくのが一般的です（3・4・6・7など）。説明では「2・3・4・5・6」と並べることにします。

数列の左端と右端にある数字を合計した金額が最初のベット額です。「2・3・4・5・6」の数列なので、2＋6＝8ドルをベットします。

勝った場合

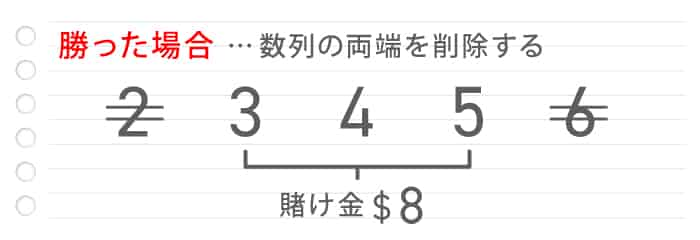
勝った場合、両端の数字を消します。

「2・3・4・5・6」の場合「3・4・5」となるので、次は3＋5＝8ドルをベットします。

負けた場合

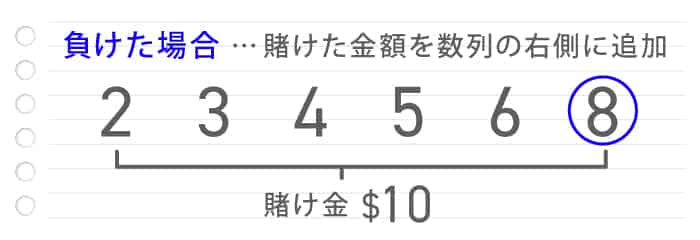
負けた場合、そのときの賭け金を数列の右端に追加します。

「2・3・4・5・6」の場合「2・3・4・5・6・8」となるので、次は2＋8＝10ドルをベットします。

勝った場合に数列が1個になったときは、その数列の数字のみベットを行います。

これを続け、数列の数字が0個になったらキャンセレーション法は成功です。この時点で、設定した目標金額分の利益が出ている状態になります。

キャンセレーション法をシミュレーションした結果

ここからのシミュレーションは、ルーレットの黒に賭け続けた場合のものです。最初の数列はセットによって異なるので、ベット額の推移をセットごとに解説します。

1セット目

まず1セット目は「2・3・4・5・6」なので合計20ドルが目標金額となります。4勝2敗という結果になりましたが、実際にすべての数列がなくなってクリアした際、20ドルの利益が出ていることが分かります。

また、モンテカルロ法では数字が1個以下になると終了ですが、キャンセレーション法では1個になっても続ける点に注意してください。

2セット目

最後は前半に負けが先行した状態のシミュレーションですが、6勝7敗ながらも20ドルの利益を出すことができました。キャンセレーション法は勝率が3分の1程度を上回るとセットを消化しやすいものの、控除率分の不利がなくなるわけではない点には注意しましょう。

このセットも一時は31ドルの負けまで沈んでいます。数列があまりにも長くなると成功の可能性は低くなるので、プレイヤーの任意のタイミングで損切りを行うとよいでしょう。当サイトおすすめの損切りラインは「最初の数列の個数から5個以上数列が増えた場合」です。

なお、同じ20ドルの目標でも数列の中身を「1・2・3・4・10」のように変えると、途中のベット額は変わりますが、消化できたときの利益は同じ20ドルです。目標額は数列の合計で決まり、分け方では変わらないためです。

キャンセレーション法のメリット

• ローリスクでもハイリスクでも対応可能
• 配当2倍のゲームなら勝率がおおむね3分の1を上回るとセットを消化しやすい
• 目標金額を自分で決められ、成功すれば設定額の利益になるので使いやすい

1回あたりのベット額は両端の数字の合計なので、「数列の合計 ÷ 個数 × 2」でおおよそ決まります。そのため同じ目標金額でも、数列を細かく分けるほど1回のベット額は小さくなります。目標金額と数列の個数の2つを自分で決められることが、このベッティングシステムの使い勝手につながっています。

また、モンテカルロ法を踏襲した仕組みのため、配当2倍のゲームでは勝率が3分の1程度を上回ると数列を消化しやすい傾向があります（ハウスエッジ分の不利は変わりません）。

キャンセレーション法のデメリット

• 長引くほどベット額が上がる
• 最初のベット額が少し高めなので連敗時のリスクは低くない
• モンテカルロ法を理解しておかないと使いづらい

キャンセレーション法は「モンテカルロ法」が元となっているベッティングシステムなので、モンテカルロ法を知らないままでは扱いが難しくなります。初めてベッティングシステムを使うプレイヤーにはややハードルが高いため、まずは基本的なものから慣れることをおすすめします。

また、1ドルほどからスタートできるベッティングシステムも多い中、キャンセレーション法はミドルリスクでも、目標金額の半分から3分の1程度のベット額が必要になります。たとえば50ドルプラスが目標の場合、スタートは20ドルくらいになるのが一般的です。そのため、1回で目標金額に到達することを目指すより、目標額を小さくして数回に分けたほうが、1セットあたりの振れ幅を抑えられます。

最後に、これはモンテカルロ法にも共通しますが、キャンセレーション法は成功せず長引いてしまうとその分ベット額が上がり、1回あたりのベットが目標金額を超えてしまう場合もあります。ときには損切りを行い、リセットしてもう一度賭け直すのも一つの手です。

キャンセレーション法を使う前に知っておくこと

キャンセレーション法を使っても、ゲームの期待値やハウスエッジ（控除率）は変わりません。変わるのは収支の振れ幅（分散）だけで、「小さな利益を高い確率で積む代わりに、低い確率で大きな損失を負う」形に収支の分布を付け替えているにすぎません。

負けるたびに数列が伸びてベット額が上がるため、連敗が続くと必要な資金は急激に増えます。目標20ドル・数列「2・3・4・5・6」で始めて5連敗すると、数列は10個に伸び、累計損失は60ドル、次のベット額は18ドルになります。当サイトの損切りライン（最初の数列より5個以上増えた場合）にちょうど到達する状態です。

テーブルリミットと手持ち資金は有限なので、数列を伸ばし続けることは必ずどこかでできなくなります。上限に達した時点で、それまでの累計損失がそのまま確定します。1セットで得られる利益は目標額に固定される一方、失敗したときの損失には上限がありません。

だからこそ、あらかじめ損切りラインを決めておくことが前提になります。ただし損切りラインを決めても期待値そのものは変わりません。1回のセッションで失う額に上限を設ける、資金管理の取り決めです。無理のない資金設定で遊んでください。

キャンセレーション法は簡単にアレンジ・改良ができる

キャンセレーション法は非常に自由度が高いベッティングシステムです。数列を分解することで、リスクを低くして長期的に戦う、もしくはすぐに成功させるために1回あたりのベット額を高くする、といったことも自在にできます。たとえば20ドルを目標とする場合、リスクごとの数列は次のように作ることができます。

ちなみに、ハイリスクの数字3個でキャンセレーション法を行った場合のシミュレーションがこちらです。

目標を20ドルに設定

ベット額は上がるものの、すぐに目標利益に達したことが分かります。このように、基本的には数列の数が少なくなるほど1回あたりのベット額が上がりハイリスクではあるものの、すぐに目標に達することが可能です。

ちなみに、ハイリスクの例として数字2個を挙げている場合がありますが、おすすめできません。たとえば「10・10」という数列の場合、最初のベットは10＋10で20ドルになります。目標利益と同額を1回で賭けることになり、数列を分割する意味がなくなるためです。

キャンセレーション法に似ているベッティングシステム

モンテカルロ法

「モンテカルロ法」は、ここまで何度か触れてきたとおり、キャンセレーション法の元となったベッティングシステムです。

操作はキャンセレーション法と同じですが、数列が1個になった時点で終了する点と、最初の数列が「1・2・3」で固定されている点が異なります。

操作の仕方が同じため、メリット・デメリットもキャンセレーション法とほぼ共通です。

ウィナーズ投資法

「ウィナーズ投資法」は、数列を使う点でキャンセレーション法と似たベッティングシステムです。

2連敗してから数列を作り始める点と、消すのが左端だけで両端ではない点が、キャンセレーション法と異なります。

連敗してもベット額が増えないため1回あたりの損失が膨らみにくく、また長引くほど成功した際の利益が大きくなる特徴があります。ただし最終的に勝率が50％を超えないとウィナーズ投資法は成功しないので、キャンセレーション法よりも条件は厳しくなります。振れ幅が小さいという意味であって、有利になるわけではありません。

まとめ：キャンセレーション法は目標額を先に決められる数列型の資金管理法

キャンセレーション法はバカラやルーレットなどで使用できるベッティングシステムで、自分で数列を考え、その数列の両端をベットしていき、モンテカルロ法の要領で数列を増やしたり消したりしていきます。最終的に数字がすべてなくなると成功となり、最初に設定した数字と同じ金額の利益を獲得できます。

目標額を自分で決められ、配当2倍のゲームでは勝率が3分の1程度を上回るとセットを消化しやすいのが特徴です。ただし変わるのは収支の振れ幅だけで、期待値もハウスエッジ（控除率）も変わりません。失敗したときの損失には上限がないため、損切りラインと無理のない目標額を先に決めたうえで使ってください。